The fundamental challenge in neuroscience lies in elucidating how the brain represents and encodes information through the activity patterns of its neuronal ensembles. This enduring quest leverages a multidisciplinary approach, integrating insights from biology, physics, chemistry, computer science, and mathematics. A transformative paradigm shift is underway, driven by the concept of the "neural manifold." This framework is not only revolutionizing our foundational understanding of neural information processing but also facilitating the development of a novel generation of high-performance Brain-Computer Interfaces (BCIs) with previously unachievable functionalities. Here we discuss the burgeoning field of neural manifolds, encompassing its theoretical foundations, computational methodologies for its identification, and its significant applications in decoding invasive BCI signals, culminating in the noteworthy accomplishment of brain-to-text communication via imagined handwriting.

The Neural Manifold Hypothesis: Discovering Simplicity in Complexity

The human brain is an organ of profound complexity, containing billions of neurons that fire in intricate, apparently chaotic patterns. The sheer number of possible neural activity states creates a "curse of dimensionality," a long-standing barrier to deciphering the brain's computational principles. The neural manifold hypothesis offers a compelling solution to this problem. It posits that the collective activity of a large neuronal population is not random but is instead constrained to a low-dimensional geometric structure, or "manifold," embedded within the high-dimensional space of all possible neural states.

An analogy can be drawn from the coordinated flight of a flock of starlings. While each bird has the freedom to move in three dimensions, the flock as a whole exhibits coherent, structured movement. The collective behavior of the flock can be described by a much smaller set of variables than the sum required to describe each individual bird. This coordinated, lower-dimensional representation is analogous to a neural manifold.

In neuroscience, the shape of this manifold is non-arbitrary; it is believed to reflect the underlying computations being performed by the neural circuit. For example, the manifold for motor control might manifest as a specific geometric object representing the full range of a limb's possible movements. A key insight, articulated by Jazayeri and Ostojic (2021), is the distinction between intrinsic dimensionality (the minimum number of variables needed to describe the system's state) and embedding dimensionality (the number of dimensions required to represent the manifold within the full neural state space). This distinction is critical, as it separates the information being encoded (the intrinsic variables) from the method of its processing and representation by the neural population (the embedding). The neural manifold hypothesis, therefore, provides a powerful conceptual framework for simplifying the complexity of neural data and uncovering the fundamental principles of neural computation.

Computational Tools for Uncovering the Mind's Geometry

The identification and analysis of neural manifolds from high-dimensional neural recordings present a significant computational challenge. Consequently, neuroscientists have developed a sophisticated toolkit of mathematical and statistical methods, each offering a unique perspective on the geometric structure of neural data.

·Principal Component Analysis (PCA): Frequently the first step in neural data analysis, PCA is a linear dimensionality reduction technique that identifies the directions of highest variance. While useful for initial exploration, PCA's linearity limits its ability to capture the complex, nonlinear geometries characteristic of many neural manifolds.

·Gaussian Process Factor Analysis (GPFA): GPFA is a more advanced method designed specifically for analyzing the temporal dynamics of neural trajectories. It integrates dimensionality reduction with a smoothing process to capture the continuous evolution of neural activity over time. This makes GPFA particularly well-suited for studying the neural basis of continuous behaviors like reaching and handwriting.

·t-Distributed Stochastic Neighbor Embedding (t-SNE): As a powerful nonlinear dimensionality reduction technique, t-SNE is primarily used for visualization. It excels at revealing the local structure of data, enabling the observation of how different neural states cluster in a low-dimensional space.

·Topological Data Analysis (TDA): A relatively new and potent approach, TDA applies concepts from algebraic topology to analyze the shape of data. TDA can identify topological features of neural manifolds, such as holes and voids, which may possess important functional significance. Its core tools are simplicial complexes, which represent data point connectivity, and persistent homology, which tracks the evolution of topological features across different scales.

These computational tools are essential for testing the neural manifold hypothesis and for extracting the information latent in complex patterns of neural activity. They permit researchers to move beyond single-neuron analysis to study the collective, emergent properties of neural populations.

The "Manifold Advantage" in BCI Decoding

The neural manifold framework has profound practical implications for the development of BCIs. By decoding from the low-dimensional manifold rather than from individual neurons, BCIs can be rendered more robust, stable, and capable of decoding more complex behaviors. This "manifold advantage" arises from several key factors:

·Robustness to Noise and Neural Variability: Neural activity is inherently noisy, and the firing patterns of individual neurons can be highly variable. The manifold represents the collective, stable state of the neural population, which is less susceptible to these fluctuations. By averaging out noise and focusing on the underlying signal, manifold-based decoding achieves a higher degree of accuracy and reliability.

·Long-Term Stability: A major hurdle for the clinical translation of BCIs has been signal instability. The activity of individual neurons can change over time, degrading BCI performance and necessitating frequent recalibration. However, research by Gallego et al. (2020) has demonstrated that neural manifolds can remain remarkably stable over long periods, even as the activity of their constituent neurons changes. This stability is a pivotal development for BCI research, opening the possibility of devices that function for extended periods without constant adjustment.

·Decoding Complex, Continuous Movements: The manifold framework is especially well-suited for decoding complex, continuous movements like handwriting and speech. These behaviors are represented by intricate trajectories on the neural manifold, which can be effectively captured and decoded by advanced machine learning models like recurrent neural networks (RNNs). This represents a significant advance over earlier BCI approaches, which were often limited to decoding simple, discrete movements.

A Landmark Application: Brain-to-Text via Imagined Handwriting

The transformative potential of the manifold-based approach is vividly illustrated by the work of Willett et al. (2021), who developed a BCI that translates imagined handwriting into text with high speed and accuracy. In this study, a participant with paralysis, who had microelectrode arrays implanted in his motor cortex, was instructed to imagine writing letters of the alphabet. The researchers employed an RNN to decode the neural activity associated with these imagined movements, training the model to recognize the unique neural trajectory on the manifold corresponding to each letter.

The results demonstrated exceptional performance: the participant was able to type at a rate of 90 characters per minute with over 99% accuracy post-autocorrection. This rate is more than double that of previous BCI typing systems and approaches the speed of able-bodied smartphone typing. A critical insight from this study is that the temporal complexity of handwriting may facilitate, rather than hinder, decoding. The rich, dynamic neural patterns associated with each letter provide a more distinctive signature for the decoder to identify. This finding has profound implications for future BCI design, suggesting a focus on decoding natural, complex behaviors over training users to control simple, artificial interfaces.

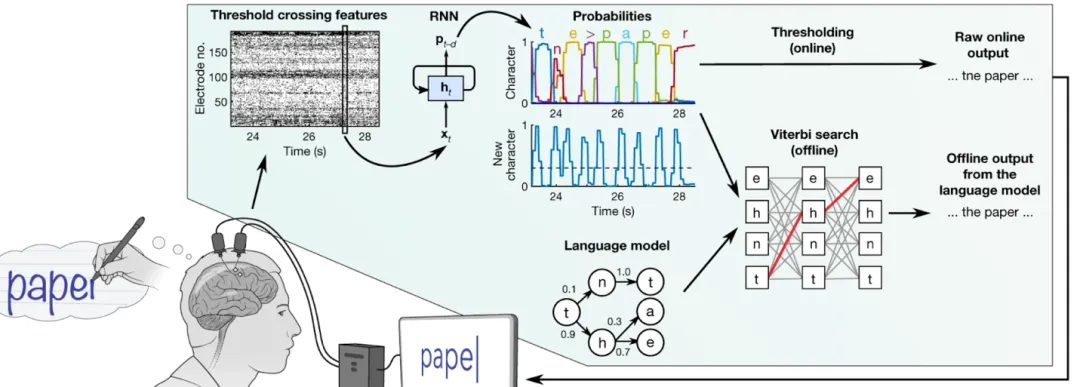
A New Generation of Decoders: Manifold-Based RNNs vs. Traditional Approaches

The manifold-based RNN approach used in the handwriting BCI represents a significant improvement over traditional BCI decoding algorithms.

·Kalman Filters: These linear decoders have been a foundational method in the BCI field. While effective for decoding simple, linear movements, they are less suited for capturing the complex, nonlinear dynamics of neural activity that underlie more sophisticated behaviors.

·Support Vector Machines (SVMs): SVMs are powerful classifiers used to distinguish between different neural states. However, they are not inherently designed to process the temporal sequences of neural data with the same efficacy as RNNs, which are specifically architected for sequential information.

In contrast, the manifold-based RNN approach learns the underlying structure of the neural code, using this knowledge to make more accurate and robust predictions. The RNN, in particular, leverages the temporal dynamics of neural trajectories on the manifold to achieve a level of performance that was previously unattainable.

The Frontier of Research: Challenges and Future Directions

Despite the remarkable progress, the field of manifold-based BCIs remains nascent, with many challenges and open questions to be addressed:

·The Problem of "Tangled" Manifolds: In some cases, the manifolds for different behaviors can become "tangled," complicating their decoding. Researchers are actively developing new computational methods for "manifold untangling," which aim to transform neural representations to make them more separable.

·Computational Complexity: Identifying and decoding from neural manifolds can be computationally intensive, posing a limitation for real-time BCI applications. The development of more efficient algorithms is a key area of ongoing research.

·Interpretability: While computational techniques can identify and visualize neural manifolds, interpreting their geometric structure to gain insight into the underlying neural computations remains a significant challenge.

Despite these challenges, the future of manifold-based BCIs is promising. Researchers are now exploring the application of this framework to other complex motor behaviors, such as speech. The development of a high-performance speech BCI would be a transformative technology for individuals who have lost the ability to speak. Furthermore, the principles of manifold-based decoding are being applied to the control of advanced prosthetic limbs, offering the potential for more natural and intuitive control for amputees.

Conclusion

The neural manifold hypothesis represents a significant shift in our understanding of the brain, providing a powerful framework for simplifying the complexity of neural data and for uncovering the fundamental principles of neural computation. This new understanding has, in turn, instigated a revolution in the field of BCIs, enabling the development of devices with unprecedented capabilities. The success of the brain-to-text handwriting BCI is a testament to the power of this approach and indicates the potential for future advances. As research continues to explore the intricate geometry of the mind, we are not only deepening our knowledge of neural function but also developing new technologies that have the potential to transform the lives of millions. The once-futuristic prospect of a seamless interface between brain and machine is now, through the science of neural manifolds, closer to reality than ever before.

References

1.Gallego, J. A., Perich, M. G., Chowdhury, R. H., Miller, L. E. & Solla, S. A. Neural manifolds for the control of movement. Neuron94, 978–984 (2017).

2.Chou, C.-N. et al. Neural manifold capacity captures representation geometry, correlations and task-efficiency across species and behaviors. In Proc. CCN 1–4 (2024).

3.Jazayeri, M. & Ostojic, S. Interpreting neural computations by examining intrinsic and embedding dimensionality of neural activity. Curr. Opin. Neurobiol.70, 1–10 (2021).

4.Langdon, C., Genkin, M. & Engel, T. A. A unifying perspective on neural manifolds and circuits for cognition. Nat. Rev. Neurosci.24, 363–377 (2023).

5.Yoon, I. H. R. et al. Tracking the topology of neural manifolds across populations. Proc. Natl Acad. Sci. USA121, e2407997121 (2024). 

6.Lin, B. & Kriegeskorte, N. The topology and geometry of neural representations. Proc. Natl Acad. Sci. USA121, e2317881121 (2024).

7.Gallego, J. A. et al. Long-term stability of cortical population dynamics underlying consistent behavior. Nat. Neurosci.23, 260–270 (2020).

8.Mitchell-Heggs, R. et al. Neural manifold analysis of brain circuit dynamics in health and disease. J. Comput. Neurosci.51, 1–21 (2023).

9.Feulner, B. & Clopath, C. Neural manifold under plasticity in a goal-driven learning behaviour. PLoS Comput. Biol.17, e1008621 (2021). 

10.Perich, M. Neural manifolds: latest buzzword or pathway to understand the brain? The Transmitter (2024).          
Fortunato, C. et al. Nonlinear manifolds underlie neural population activity during behaviour. bioRxiv 2023.07.18.549575 (2023).

11.Ma, H., Jiang, L., Liu, T. & Liu, J. From sensory to perceptual manifolds: the twist of neural geometry. bioRxiv 2023.10.02.559721 (2023).          
Neuromatch Academy. Week 1 Day 4: Dimensionality reduction – Intro.https://compneuro.neuromatch.io/tutorials/W1D4_DimensionalityReduction/student/W1D4_Intro.html (2025). 

12.Hasnain, M. Dimensionality reduction for neural data analysis. Chand Lab Blog, Boston University (2020).