讲透一个强大算法模型，Transformer ！！

机器学习和人工智能AI
2025-07-20 15:36:00

哈喽，大家好~

咱们今天结合ARIMA，好好聊聊Transformer与ARIMA结合的混合时间序列建模问题~

传统的方法（比如ARIMA）像是用老式温度计，比较擅长抓住天气的总体趋势和季节性变化，也就是那种“直觉上认为今天比昨天热一点”的感觉。但天气其实既有简单的趋势，也有一些突发的、复杂的变化。

Transformer 就像是一个“超级侦探”，能通过分析大量历史数据找出隐藏在数据中的复杂模式和依赖关系，尤其是那些非线性的、看起来有点“捉摸不定”的变化。

当你把两者结合时，思路是这样的：

先用ARIMA：捕捉数据中明显的线性变化（比如稳定上升或周期性波动）。
再用Transformer：对ARIMA预测后的“剩余部分”（也就是残差），去挖掘那些复杂、非线性的信号。

最终，两部分相加，就能得到一个既考虑了传统统计规律，又捕捉了深层复杂模式的预测结果。

1. ARIMA模型

ARIMA 模型（AutoRegressive Integrated Moving Average）是一种经典的统计时间序列模型，它适用于平稳或经过差分处理后的平稳数据。

ARIMA 模型通过三个部分描述时间序列：

**自回归 (AR)**：利用过去的值来预测当前值；
**差分 (I, Integrated)**：对数据进行差分处理以消除趋势，使序列平稳；
**移动平均 (MA)**：用过去的预测误差来修正当前的预测。

核心公式：

一般记为 ARIMA(p, d, q)，其数学表达式为

其中：

是时间序列在时刻的值。
是后移算子，即。
表示自回归部分。
表示移动平均部分。
表示需要进行几次差分以达到平稳性。
是白噪声误差项。

推理过程：

首先，对原始数据进行平稳性检验（例如单位根检验），必要时进行差分处理（差分阶数为）。
根据自相关函数（ACF）和偏自相关函数（PACF）的图形确定合适的 p（AR阶数）和 q（MA阶数）。
利用历史数据估计模型参数和，构建 ARIMA 模型。
最终得到对线性部分的预测值。

2. Transformer模型

Transformer 模型最初用于自然语言处理，其优势在于自注意力机制（Self-Attention），能够捕捉序列数据中任意位置之间的关系。对于时间序列任务，Transformer 能够通过多头注意力机制，挖掘出复杂的非线性依赖和长距离关联特征。

核心公式：

最基础的自注意力机制公式为

其中：

（Query）、（Key）、（Value）分别由输入经过线性变换得到。
是 Key 的维度，用于缩放，防止点积值过大导致梯度消失或梯度爆炸。
通过多个注意力头（Multi-Head Attention），模型可以从多个子空间中捕捉信息。

推理过程：

输入时间序列数据经过嵌入层和位置编码后，传入 Transformer 的编码器（Encoder）。
在每个编码器层中，通过多头注意力机制和前馈神经网络（Feed Forward Network）提取和融合时序信息。
Transformer 能捕捉到数据中隐藏的非线性变化模式，从而对残差进行建模。

3. 混合模型的组合思路

时间序列数据通常可以分解为两部分：

线性部分：由 ARIMA 模型捕捉。
非线性部分：由 Transformer 模型捕捉。

组合公式：

ARIMA 部分：
用 ARIMA 模型预测线性成分，得到预测值
残差计算：
残差表示 ARIMA 模型未捕捉到的非线性成分，
Transformer 部分：
使用 Transformer 模型对残差序列进行建模，得到预测残差
最终预测：
将两部分相加得到最终预测结果

整体推理流程：

步骤一： 数据预处理，检查平稳性，对必要的部分进行差分，构建 ARIMA 模型并预测线性趋势。
步骤二： 计算 ARIMA 模型预测后的残差序列。
步骤三： 构建并训练 Transformer 模型，利用自注意力机制捕捉残差中的复杂非线性模式。
步骤四： 将 ARIMA 的预测结果与 Transformer 对残差的预测相加，得到最终预测结果。

这种混合方法能够发挥两种模型的优势：ARIMA 处理线性和周期性成分，Transformer 捕捉复杂的、非线性的依赖关系，从而提升整体预测精度。

完整案例

在时间序列预测中，我们常常会遇到这样一种现象：数据同时包含明显的线性趋势、周期性波动以及复杂的非线性成分。传统的统计模型如ARIMA对平稳序列建模较好，能够捕捉线性趋势、周期性变化和季节性模式，但当面对数据中潜藏的非线性关系时，其表现往往受限。另一方面，Transformer 凭借其自注意力机制，可以捕捉序列数据中任意位置之间的长程依赖和复杂的非线性关系，然而直接用Transformer对原始时间序列进行建模，往往需要大量数据和较高的计算成本，且在处理短期局部变化时可能不如统计模型稳定。

因此，一种常见且有效的思路是采用混合建模方法：先利用ARIMA模型拟合出数据中的线性趋势和周期性成分，再利用Transformer捕捉ARIMA模型拟合后残差中的非线性细节。这样既能发挥ARIMA在传统时间序列分析中的优势，也能利用Transformer捕捉到非线性部分的复杂特征，从而使整体预测效果大大提升。

代码中每一步均添加了详细注释，帮助理解各个模块的实现，大家可以自己动手实现~

import numpy as np
import matplotlib.pyplot as plt
import torch
import torch.nn as nn
import torch.optim as optim
from torch.utils.data import Dataset, DataLoader
from statsmodels.tsa.arima.model import ARIMA
import warnings

# 忽略statsmodels的警告信息
warnings.filterwarnings("ignore")

# 1. 数据生成与预处理
# 为确保结果可复现，设置随机种子
np.random.seed(42)
torch.manual_seed(42)

def generate_synthetic_data(n=1000):
    """
    构造虚拟时间序列数据，包含线性趋势、周期性波动、非线性平滑变化及随机噪声
    """
    t = np.arange(n)
    # 线性趋势部分
    trend = 0.05 * t
    # 周期性部分：使用正弦函数模拟周期波动
    seasonal = 10 * np.sin(0.2 * t)
    # 非线性平滑变化：使用tanh函数模拟
    nonlinear = 5 * np.tanh(0.01 * (t - 500))
    # 加入随机噪声，服从正态分布（均值0，标准差2）
    noise = np.random.normal(0, 2, n)
    # 最终数据为各部分之和
    y = trend + seasonal + nonlinear + noise
    return t, y

# 生成虚拟数据
t, y = generate_synthetic_data(n=1000)

# 2. ARIMA模型建模与残差提取
print("开始ARIMA模型拟合……")
# 采用ARIMA(2,1,2)模型，进行一阶差分处理
model = ARIMA(y, order=(2, 1, 2))
arima_result = model.fit()
# 获取ARIMA拟合值（由于差分的原因，拟合值索引可能与原始数据不完全对齐）
arima_pred = arima_result.fittedvalues

# 对齐数据：由于差分处理，填充第一个缺失值为NaN
arima_pred_full = np.concatenate(([np.nan], arima_pred))
# 计算残差：真实值减去ARIMA预测值
arima_pred_full = arima_pred  # 如果长度已匹配
residuals_full = y - arima_pred_full

# 仅保留有效数据（去除NaN部分）
valid_index = ~np.isnan(arima_pred_full)
t_valid = t[valid_index]
y_valid = y[valid_index]
arima_pred_valid = arima_pred_full[valid_index]
residuals_valid = residuals_full[valid_index]

# 3. 构造Transformer训练数据（残差序列）
class ResidualDataset(Dataset):
    def __init__(self, residuals, seq_len):
        self.residuals = residuals
        self.seq_len = seq_len

    def __len__(self):
        return len(self.residuals) - self.seq_len

    def __getitem__(self, idx):
        # 取连续的seq_len个数据作为输入
        x = self.residuals[idx: idx + self.seq_len]
        # 下一个时间步的残差作为标签
        y_label = self.residuals[idx + self.seq_len]
        # 增加特征维度（即1维）
        return torch.tensor(x, dtype=torch.float32).unsqueeze(-1), torch.tensor(y_label, dtype=torch.float32)

# 设置滑动窗口长度
seq_len = 20
dataset = ResidualDataset(residuals_valid, seq_len)
dataloader = DataLoader(dataset, batch_size=32, shuffle=True)

# 4. 构造Transformer残差预测模型
class PositionalEncoding(nn.Module):
    """
    位置编码模块：将位置信息添加到输入数据中
    """
    def __init__(self, d_model, dropout=0.1, max_len=500):
        super(PositionalEncoding, self).__init__()
        self.dropout = nn.Dropout(p=dropout)
        # 初始化位置编码矩阵，形状为(max_len, d_model)
        pe = torch.zeros(max_len, d_model)
        position = torch.arange(0, max_len, dtype=torch.float).unsqueeze(1)
        div_term = torch.exp(torch.arange(0, d_model, 2, dtype=torch.float) * (-np.log(10000.0) / d_model))
        pe[:, 0::2] = torch.sin(position * div_term)
        if d_model % 2 == 1:
            pe[:, 1::2] = torch.cos(position * div_term)[:, :pe[:, 1::2].shape[1]]
        else:
            pe[:, 1::2] = torch.cos(position * div_term)
        pe = pe.unsqueeze(0)  # shape: (1, max_len, d_model)
        self.register_buffer('pe', pe)

    def forward(self, x):
        # x: (batch, seq_len, d_model)
        x = x + self.pe[:, :x.size(1)]
        return self.dropout(x)

class TransformerResidual(nn.Module):
    """
    Transformer残差预测模型：
    输入为一段残差序列，经过线性升维、位置编码、Transformer Encoder，
    最后通过全连接层输出下一个时间步的预测残差
    """
    def __init__(self, input_dim=1, d_model=64, nhead=4, num_layers=2, dim_feedforward=128, dropout=0.1, seq_len=20):
        super(TransformerResidual, self).__init__()
        # 线性升维层
        self.input_linear = nn.Linear(input_dim, d_model)
        # 位置编码层
        self.pos_encoder = PositionalEncoding(d_model, dropout, max_len=seq_len)
        # Transformer编码器层
        encoder_layer = nn.TransformerEncoderLayer(d_model, nhead, dim_feedforward, dropout)
        self.transformer_encoder = nn.TransformerEncoder(encoder_layer, num_layers)
        # 解码层，将Transformer输出映射为标量预测值
        self.decoder = nn.Linear(d_model, 1)

    def forward(self, src):
        """
        src: (batch, seq_len, 1)
        """
        src = self.input_linear(src)  # 变换为 (batch, seq_len, d_model)
        src = self.pos_encoder(src)
        # Transformer要求输入形状为 (seq_len, batch, d_model)
        src = src.transpose(0, 1)
        output = self.transformer_encoder(src)
        # 取最后一时刻的输出作为序列表示
        output = output[-1]
        output = self.decoder(output)
        return output.squeeze(-1)

# 5. Transformer模型训练
# 初始化模型、损失函数和优化器
model_transformer = TransformerResidual(seq_len=seq_len)
criterion = nn.MSELoss()
optimizer = optim.Adam(model_transformer.parameters(), lr=0.001)

print("开始Transformer模型训练……")
num_epochs = 50
losses = []

for epoch in range(num_epochs):
    epoch_loss = 0.0
    for batch_x, batch_y in dataloader:
        optimizer.zero_grad()
        pred = model_transformer(batch_x)
        loss = criterion(pred, batch_y)
        loss.backward()
        optimizer.step()
        epoch_loss += loss.item() * batch_x.size(0)
    epoch_loss /= len(dataset)
    losses.append(epoch_loss)
    if (epoch + 1) % 10 == 0:
        print(f'Epoch {epoch+1}/{num_epochs}, Loss: {epoch_loss:.4f}')

# 6. 利用训练好的Transformer模型预测残差
model_transformer.eval()
transformer_preds = []
# 遍历整个数据集（滑动窗口方式预测）
with torch.no_grad():
    for i in range(len(dataset)):
        x, y_val = dataset[i]
        x = x.unsqueeze(0)  # 添加batch维度
        pred = model_transformer(x)
        transformer_preds.append(pred.item())
transformer_preds = np.array(transformer_preds)

# 7. 混合模型预测结果合成
# 由于Transformer预测从第seq_len个数据点开始，因此对应ARIMA预测数据也需对齐
combined_pred = arima_pred_valid[seq_len:] + transformer_preds
t_final = t_valid[seq_len:]
y_final = y_valid[seq_len:]

# 8. 综合数据分析图形
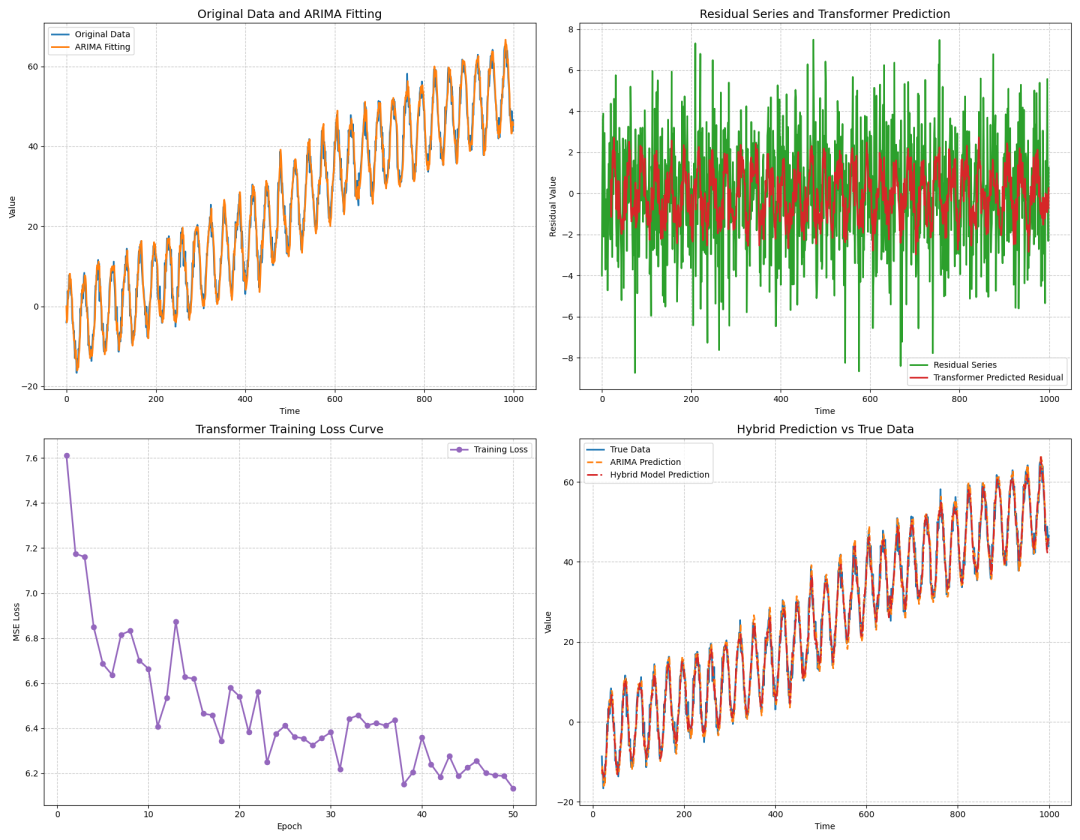
# (a) Original Data and ARIMA Fitting
# (b) Residual Series and Transformer Predicted Residual
# (c) Transformer Training Loss Curve
# (d) Final Hybrid Prediction vs True Data

fig, axs = plt.subplots(2, 2, figsize=(18, 14))

# Subplot (a): Original Data and ARIMA Fitting
axs[0, 0].plot(t, y, label='Original Data', color='tab:blue', linewidth=2)
axs[0, 0].plot(t_valid, arima_pred_valid, label='ARIMA Fitting', color='tab:orange', linewidth=2)
axs[0, 0].set_title('Original Data and ARIMA Fitting', fontsize=14)
axs[0, 0].set_xlabel('Time')
axs[0, 0].set_ylabel('Value')
axs[0, 0].legend()
axs[0, 0].grid(True, linestyle='--', alpha=0.7)

# Subplot (b): Residual Series and Transformer Predicted Residual
axs[0, 1].plot(t_valid, residuals_valid, label='Residual Series', color='tab:green', linewidth=2)
axs[0, 1].plot(t_valid[seq_len:], transformer_preds, label='Transformer Predicted Residual', color='tab:red', linewidth=2)
axs[0, 1].set_title('Residual Series and Transformer Prediction', fontsize=14)
axs[0, 1].set_xlabel('Time')
axs[0, 1].set_ylabel('Residual Value')
axs[0, 1].legend()
axs[0, 1].grid(True, linestyle='--', alpha=0.7)

# Subplot (c): Transformer Training Loss Curve
axs[1, 0].plot(range(1, num_epochs + 1), losses, marker='o', label='Training Loss', color='tab:purple', linewidth=2)
axs[1, 0].set_title('Transformer Training Loss Curve', fontsize=14)
axs[1, 0].set_xlabel('Epoch')
axs[1, 0].set_ylabel('MSE Loss')
axs[1, 0].legend()
axs[1, 0].grid(True, linestyle='--', alpha=0.7)

# Subplot (d): Final Hybrid Prediction vs True Data
axs[1, 1].plot(t_final, y_final, label='True Data', color='tab:blue', linewidth=2)
axs[1, 1].plot(t_final, arima_pred_valid[seq_len:], label='ARIMA Prediction', color='tab:orange', linestyle='--', linewidth=2)
axs[1, 1].plot(t_final, combined_pred, label='Hybrid Model Prediction', color='tab:red', linestyle='-.', linewidth=2)
axs[1, 1].set_title('Hybrid Prediction vs True Data', fontsize=14)
axs[1, 1].set_xlabel('Time')
axs[1, 1].set_ylabel('Value')
axs[1, 1].legend()
axs[1, 1].grid(True, linestyle='--', alpha=0.7)

plt.tight_layout()
plt.show()

Subplot (a): Original Data and ARIMA Fitting：展示原始数据与ARIMA模型拟合结果，直观反映ARIMA对整体趋势与周期性波动的拟合效果。
Subplot (b): Residual Series and Transformer Prediction：展示ARIMA残差序列和Transformer预测的残差，说明Transformer能捕捉残差中未被ARIMA拟合的非线性信息。
Subplot (c): Transformer Training Loss Curve：展示Transformer训练过程中的损失变化，验证模型收敛情况与训练稳定性。
Subplot (d): Hybrid Prediction vs True Data：展示混合模型预测结果与真实数据对比，以及单独ARIMA预测结果，说明混合模型在细节修正方面的优势，特别是在非线性波动剧烈的区域，混合模型更贴近真实数据。

整个内容，给大家聊了聊构建并实现“Transformer与ARIMA结合的混合时间序列预测”模型。从数据集构造、ARIMA模型拟合、残差提取，到基于Transformer模型的残差预测，再到最终混合预测结果的生成与可视化展示，

当然，每一步都进行了细致的解释与代码实现说明。大家可以复现起来~

最后

最近准备了16大块的内容，124个算法问题的总结，完整的机器学习小册，免费领取~

领取：备注「算法小册」即可~

声明：本文内容及配图由入驻作者撰写或合作网站授权转载。文章观点仅代表作者本人，不代表科技区角网立场。仅供工程师学习之用，如有内容侵权或者其他违规问题，请联系本站处理。点击这里

点赞 (0)
分享
微信扫一扫
加入群聊
扫码加入群聊