将 ScienceAI 设为星标

第一时间掌握

新鲜的 AI for Science 资讯

编辑 | 白菜叶

在分子与材料性质的模拟中，电子结构计算的高精度往往伴随着高昂的计算成本。

目前，从头算方法（ab initio）能够精确描述多体电子波函数，但其庞大的计算量限制了实际应用。

问题的复杂性还体现在弱关联系统与强关联系统的模糊分界上。

对于弱关联系统（如平衡态分子），耦合团簇（CC）等单参考方法能高效且高精度地求解波函数。然而，这类系统仅是化学空间中的一座「孤岛」，其边界尚未明确。

而对于强关联系统（如过渡金属化合物或反应过渡态），现有方法缺乏统一标准，往往需要专家手动调整，且多参考方法的计算成本更高。

计算化学的挑战，本质上是一场在精度与效率之间的艰难平衡。

在这里，微软研究院 AI for Science 团队（Microsoft Research AI for Science）、德国柏林自由大学（Freie Universität Berlin）的研究人员利用 Orbformer 这一新范式来应对这一挑战。

相关论文《An ab initio foundation model of wavefunctions that accurately describes chemical bond breaking》已经发布在 arXiv 预印平台。

Orbformer 是一种新型的可转移波函数模型，可针对未知分子进行微调，从而达到可与经典多参考方法媲美的准确率成本比。在现有基准以及更具挑战性的键解离和狄尔斯-阿尔德反应中，Orbformer 是唯一能够始终收敛到化学精度（1 kcal/mol）的方法。

这项工作将「在多个分子上分摊薛定谔方程求解成本」的理念变成了量子化学中的实用方法。

Orbformer 适用于不同大小、组成和几何形状的分子，但可以达到甚至超越与最先进的单点拟设相同的能量精度；它能够学习可组合的分子特征，然后推广到更多不同的分子中。

图示：Orbformer 预训练和微调。（来源：论文）

具体而言，Orbformer 能够同时近似解出各种分子的电子薛定谔方程。该模型接受分子构型 M 和电子的空间自旋坐标 x 作为输入。

将 M 作为波函数网络的输入，而不是描述优化问题的参数，是他们实现相似分子间计算共享的核心方法。

Orbformer 由 Jastrow 因子和广义 Slater 行列式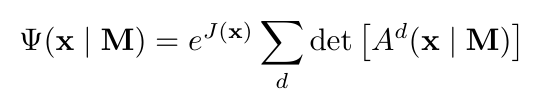之和构成，确保对于每个 M，作为 x 函数的模型都是有效的反对称波函数。

Orbformer 的架构与模块

图示：Orbformer 的架构与模块。（来源：论文）

1. Nuclei Message Passing Neural Network (MPNN)

输入: 分子构型 M 

输出: 

(1) 原子核特征矩阵 Q_nf^nuc(用于 Orbital Generator 的消息传递）

(2) 旋转矩阵W_n^rot (用于 Electron Transformer 的电子-原子核特征提取）

2. Orbital Generator动态轨道生成器（比Nuclei MPNN多一个orbital axis）

输入：

(1) 电子坐标 r_e + 核坐标 R_n;

(2) Electron Transformer 输出的电子特征 Tef

输出：

(1) 局域化轨道包络 (Envelopes, Ω); 

(2) 投影电子表示（Projected Electron Representations, Φ) 

突破与创新：

Ω: (1) 无需预设轨道类型，通过变分原理自动学习局域化模式（如碳原子的双局域轨道）。(2) 指数衰减保证远距离相互作用趋近于零，满足组合性（composability）约束。

Φ: (1) 严格推广经典轨道概念：Φ 依赖所有电子坐标（通过Transformer的全连接注意力），而非常规单电子轨道。(2) 动态参数化：权重 Wrepr 由分子构型 M 动态生成，使轨道可迁移至不同分子。(3) 组合性保障：当分子解离时，Φ 矩阵退化为块对角形式，确保轨道在相似化学环境中复用。

3. Electron Transformer 多电子关联建模引擎（物理可解释架构）

输入: 

(1) 电子坐标与自旋 x; 

(2) 分子构型 M的旋转矩阵W_n^rot (来自 Nuclei MPNN)

输出: 

电子特征矩阵 Tef: 用于构建 Orbital Generator 中的投影表示 Φd (广义Slater矩阵 Ad=Ωd⊙Φd的核心组分); 满足电子置换等变性

突破与创新: 

(1) 核感知的特征提取: 通过两种 filter 函数（指数型，sigmoid 型）以实现(a) 在 r→0(电子近核）时梯度非零[满足 Kato cusp 条件](b) 在 r→∞时趋近于0 [更好实现composability] 

(2) 物理约束的注意力机制(距离衰减bias函数): 强制注意力权重随电子间距离增大而指数衰减（attention∝exp(−r))，确保远距离电子无相互作用，满足 size consistency 要求

(3) 接收门控（receiver gate): 允许近核电子屏蔽远距离电子的干扰更新，增强轨道局域性且不损害表达能力。

注意，这里也和Psiformer一样使用了tanh-activated MLP，并且使用了FlashAttention进行加速计算

Nuclei MPNN, Orbital GeneratorElectron Transformer 三大模块通过几何-电子信息流，共同实现：

组合性（Composability）：Nuclei MPNN 的距离衰减 → Orbital Generator 的轨道局域化 → Electron Transformer 的注意力衰减→ 解离时 Slater 矩阵自动退化为块对角形式。

可迁移性（Transferability）：轨道参数由分子构型动态生成 → 同一套模型参数泛化至不同分子和构象。

多参考精度：Electron Transformer 的全电子关联建模 + 多行列式求和 → 精确描述键断裂/过渡态。

该拟设设计的一个指导原则是局域性——任意两个粒子之间的相互作用都经过精心设计，使其随着距离的增加而衰减，并且轨道生成器被限制为只产生局域轨道。研究人员证明，当不同的分子中出现相似的化学环境时，这将有助于轨道的重复利用。

研究人员训练 Orbformer 波函数来最小化哈密顿算子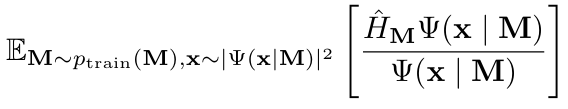的期望值（能量），其中期望值取自从训练分布中采样的分子配置和从当前模型定义的非正则化分布中采样的电子坐标。

这种自生成方案除了选择分子训练分布外，不需要任何外部输入数据。这里研究人员的设置通过对分子构型添加外部期望，推广了标准变分蒙特卡洛 (VMC)。

Orbformer 的计算成本摊销源于化学预训练和可迁移微调的结合。在预训练过程中，研究人员向模型提供一组极其多样化的分子，并进行变分训练，以将大量化学空间的电子结构编码到半定量水平。

研究人员专门创建了一个包含 22,350 个分子构型的预训练数据集，这些构型最多包含 24 个电子，由 H、Li、B、C、N、O、F 以各种几何构型组成。

该 Light Atom Curriculum（LAC）数据集专为涉及多参考非平衡几何结构而设计。为了最大限度地提高速度和稳定性，研究人员分三个阶段进行预训练，规模/复杂度依次递增，如下图所示。他们在深度 QMC 训练协议中引入了创新，从而辅助高效的大规模训练。

图示：使用 LAC 数据集进行 Orbformer 化学预训练的阶段。（来源：论文）

为了获得高精度的波函数，研究人员从预训练模型开始，进行微调直至收敛。当然，他们并不对每个结构进行单独微调，而是将目标结构分组，同时使用一组模型参数对它们进行微调。例如，研究人员通常会使用同一组原子核对所有几何形状进行微调。这种方法的摊销可以降低成本，该成本与几何形状的数量成比例。

性能强悍

性能方面，Orbformer 在狄尔斯-阿尔德反应过渡态的计算结果与实验结果高度一致。

图示：标志性狄尔斯-阿尔德反应的活化能和反应能的准确性。（来源：论文）

与 DFT、NEVPT2、MRCI 和 MRCC 等经典方法相比，Orbformer 在五键解离曲线的计算中展现出成本与精度之间的良好平衡，并且可以通过更精细的调整进行系统性改进，而经典方法的收敛并不总是那么简单。

与早期的深度量子蒙特卡洛 (QMC) 方法相比，该团队的创新将达到化学精度的成本降低了约两个数量级（相对于最佳单点计算而言），并使 Orbformer 比早期的化学可迁移模型更加精确，并且从预训练中获益更多。

该模型直接从变分原理中学习电子结构的可识别特征，例如每个碳原子恰好存在两个局域「核心」轨道，而无需将这些特征硬编码到模型架构中。

结语

Orbformer 首次证明了通过对神经网络波函数模型进行预训练和可迁移微调，在高精度量子化学中大规模摊销计算成本的可能性。

该团队发现 Orbformer 与传统波函数方法相比更具竞争力，不仅因为它最终的精度更高，还因为它能够实现良好的成本-精度平衡。

这完全是因为通过学习利用不同分子和几何结构的电子波函数中重复出现的模式，大幅降低了每个结构的计算成本。

对于大规模使用，研究人员设想将 Orbformer 视为一种更便宜的模型的数据生成方法，例如适用于多参考系统的反应力场。

Orbformer 的出现，虽然并非故事的终点，但它标志着在构建一个概括分子电子结构的模型方面取得了重大进展。鉴于其在多参考问题中具有良好的成本与精度平衡，Orbformer 必将成为当今量子化学应用的有力工具。

论文链接：https://arxiv.org/abs/2506.19960

相关内容：https://mp.weixin.qq.com/s/Dc0RItibTAJ0ooGLQWpEJg